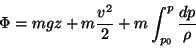


suivant: La conductivité hydraulique et
monter: Le milieu souterrain et
précédent: Les formations perméables/imperméables
Table des matières
Sous-sections
L'écoulement de l'eau à travers les formations perméables a
été étudié par Darcy en 1856. L'expérience qui est à
l'origine de la loi de Darcy est la suivante:
Considérons un cylindre de section 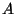 , rempli de sable, avec une
circulation d'eau et deux manomètres, figure 19. L'eau est
introduite dans le cylindre, sature les pores avant de s'écouler à
l'autre extrémité.
fig19.eps
En prenant un niveau de référence
, rempli de sable, avec une
circulation d'eau et deux manomètres, figure 19. L'eau est
introduite dans le cylindre, sature les pores avant de s'écouler à
l'autre extrémité.
fig19.eps
En prenant un niveau de référence 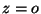 , on attribue
, on attribue 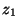 et
et 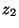 aux
niveaux des ouvertures des manomètres et
aux
niveaux des ouvertures des manomètres et 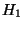 et
et 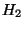 [m] aux hauteurs du
fluide.
Le débit total traversant le cylindre est noté
[m] aux hauteurs du
fluide.
Le débit total traversant le cylindre est noté 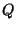 [m
[m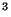 s
s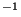 ].
On définira alors
].
On définira alors 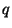 ou
ou 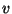 , comme le débit spécifique à travers
le cylindre:
, comme le débit spécifique à travers
le cylindre:
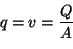 |
(3.1) |
Le débit spécifique a la dimension d'une vitesse [ms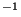 ].
On observe que
].
On observe que 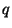 est directement proportionnel à
est directement proportionnel à 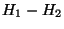 si la
distance
si la
distance 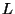 entre les manomètres 1 et 2 est
constante et inversement proportionnel à
entre les manomètres 1 et 2 est
constante et inversement proportionnel à 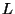 , si
, si 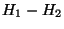 est constant.
Si on définit
est constant.
Si on définit 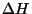 comme
comme 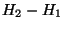 , alors la loi de
Darcy s'écrit:
, alors la loi de
Darcy s'écrit:
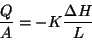 |
(3.2) |
ou
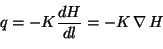 |
(3.3) |
On appelle 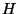 la charge hydraulique et
la charge hydraulique et 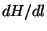 est le gradient hydraulique.
est le gradient hydraulique.
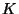 est une constante de proportionnalité qui est fonction, entre
autres, de la nature du sable dans le cylindre. On appelle
est une constante de proportionnalité qui est fonction, entre
autres, de la nature du sable dans le cylindre. On appelle 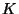 la
conductivité hydraulique (ou le coefficient de
perméabilité). Elle a la dimension d'une vitesse.
On peut également exprimer Darcy, sur la base du débit:
la
conductivité hydraulique (ou le coefficient de
perméabilité). Elle a la dimension d'une vitesse.
On peut également exprimer Darcy, sur la base du débit:
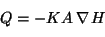 |
(3.4) |
Une notation usuelle est de noté 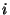 le gradient de charge. On a
alors
le gradient de charge. On a
alors
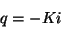 |
(3.5) |
La loi de Darcy est valable quelque soit la direction du cylindre de
sable. Si 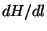 et
et 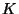 sont maintenus constants,
sont maintenus constants, 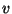 est indépendant de
l'angle.
On appelle quelquefois le débit spécifique ou unitaire, la vitesse
de Darcy ou la vitesse de filtration,
est indépendant de
l'angle.
On appelle quelquefois le débit spécifique ou unitaire, la vitesse
de Darcy ou la vitesse de filtration, 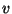 . Mais cette vitesse est
parfaitement fictive et il est préférable de ne parler que du
débit spécifique.
Tout déplacement de fluide implique l'existence d'un gradient de
potentiel (ex.: électricité, chaleur). En ce qui concerne le
déplacement de l'eau dans un milieu poreux, Hubbert a démontré
en 1940 que le potentiel de l'eau correspond à l'énergie
mécanique par unité de masse.
On établit en suivant la démonstration de Freeze et Cherry
(fig. 20) que le potentiel hydraulique
. Mais cette vitesse est
parfaitement fictive et il est préférable de ne parler que du
débit spécifique.
Tout déplacement de fluide implique l'existence d'un gradient de
potentiel (ex.: électricité, chaleur). En ce qui concerne le
déplacement de l'eau dans un milieu poreux, Hubbert a démontré
en 1940 que le potentiel de l'eau correspond à l'énergie
mécanique par unité de masse.
On établit en suivant la démonstration de Freeze et Cherry
(fig. 20) que le potentiel hydraulique 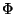 est égal à trois types de
travail:
est égal à trois types de
travail:
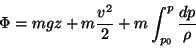 |
(3.6) |
avec
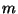 = 1
= 1
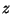 = altitude
= altitude
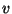 = vitesse
= vitesse
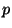 = pression
= pression
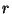 = masse volumique (unité, voir fig. 20)
= masse volumique (unité, voir fig. 20)
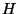 = charge hydraulique
= charge hydraulique
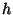 = pression au-dessus d'un point
= pression au-dessus d'un point
Et on observe que le potentiel hydraulique en n'importe quel point est
égal à la charge hydraulique multipliée par l'accélration de
la pesanteur 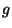 , fig. 20, (2.4)
, fig. 20, (2.4)
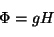 |
(3.7) |
et
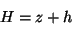 |
(3.8) |
L'eau se déplace donc selon les gradients de potentiel (du point à
haute énergie vers le point à basse énergie) ou de charge
hydraulique. Le gradient de charge hydraulique exprime la perte de
charge le long d'une ligne de courant, soit la perte de pression ou
d'altitude le long d'une ligne d'écoulement.



suivant: La conductivité hydraulique et
monter: Le milieu souterrain et
précédent: Les formations perméables/imperméables
Table des matières
2002-08-27