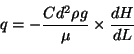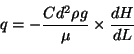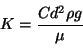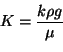


suivant: Valeurs de la conductivité
monter: Le milieu souterrain et
précédent: L'écoulement dans les milieux
Table des matières
Dans le cylindre de l'expérience de Darcy, il est évident que si
l'eau est remplacée par un fluide plus visqueux, le débit
spécifique sera différent, plus faible.
Ainsi si on fait varier la masse volumique 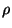 et la viscosité
dynamique
et la viscosité
dynamique 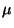 on verra que
on verra que 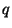 varie directement en fonction de
varie directement en fonction de
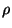 et indirectement en fonction de
et indirectement en fonction de 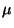 .
La loi de Darcy devient:
.
La loi de Darcy devient:
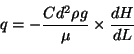 |
(3.9) |
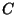 est un nouveau facteur de proportionnalité fonction de la
distribution et de la sphéricité des grains,
est un nouveau facteur de proportionnalité fonction de la
distribution et de la sphéricité des grains, 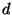 (
(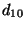 ) exprime le
diamètre des grains en [m].
) exprime le
diamètre des grains en [m].
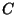 a une valeur de l'ordre de 6.54 10
a une valeur de l'ordre de 6.54 10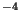 .
Ainsi
.
Ainsi
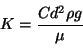 |
(3.10) |
ou
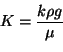 |
(3.11) |
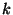 représente la perméabilité [m
représente la perméabilité [m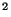 ], on la dénome
aussi perméabilité intrinsèque ou spécifique car elle ne
dépend que de la structure et de la connectivité des pores et non
du fluide se déplacant dans les pores.
], on la dénome
aussi perméabilité intrinsèque ou spécifique car elle ne
dépend que de la structure et de la connectivité des pores et non
du fluide se déplacant dans les pores.
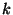 est exprimée en m
est exprimée en m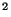 ou cm
ou cm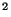 ;
; 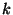 est très faible d'où l'emploi du
Darcy; 1 Darcy vaut 10
est très faible d'où l'emploi du
Darcy; 1 Darcy vaut 10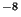 cm
cm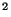 , 10
, 10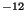 m
m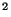 .
On peut estimer
.
On peut estimer 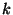 à partir de la granulométrie d'un milieu poreux
(équation de Hazen):
à partir de la granulométrie d'un milieu poreux
(équation de Hazen):
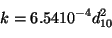 |
(3.12) |
On voit donc que la conductivité hydraulique 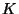 peut varier en
fonction de la densité et de la viscositde l'eau. Le facteur de
la température joue ainsi un grand rôle et les eaux chaudes sont
courantes en hydrogéologie, figure 21.
Quand T = 5
peut varier en
fonction de la densité et de la viscositde l'eau. Le facteur de
la température joue ainsi un grand rôle et les eaux chaudes sont
courantes en hydrogéologie, figure 21.
Quand T = 5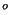 C,
C, 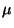 = 0.015 poise et quand T = 30
= 0.015 poise et quand T = 30 C,
C, 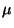 =
0.007 poise.
fig21.eps
=
0.007 poise.
fig21.eps



suivant: Valeurs de la conductivité
monter: Le milieu souterrain et
précédent: L'écoulement dans les milieux
Table des matières
2002-08-27