Les systèmes d'écoulement

Formulation de l'écoulement souterrain

Les équations différentielles de l'écoulement (et du transport de masse) sont des expressions mathématiques exprimant la "conservation de la masse" combinées au processus de déplacement de l'eau sous l'effet d'un gradient (loi de Darcy). En utilisant la divergence (différence dans un volume bien déterminé du milieu entre la quantité d'eau qui entre et qui sort), on obtient l'équation de la continuité, équation qui prend, pour une nappe captive, la forme suivante en 3D:

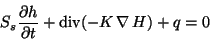$$S_s \pd{h}{t} + \Div( -K \grad H ) + q = 0$$ (4.11)

En 2D, elle s'exprime ainsi:

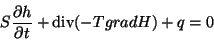$$S \pd{h}{t} + \Div (-T grad H) + q = 0$$ (4.12)

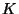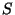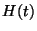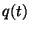Pour simuler des écoulements, il faut donc définir la région étudiée, établir les champs de $K$ et de $S$, imposer des conditions aux limites $H(t)$ ou $q(t)$ et fixer des conditions initiales 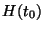$H(t_0)$ des points de la région étudiée.

Observations en laboratoire fictif

Soit un bac rempli de sable, dont la surface est en pente. Sa conductivité hydraulique est en principe identique en toutes directions et ses limites verticales et horizontales sont imperméables. Un système d'arrosage régulier de sa surface induit une saturation du bac dont la surface libre de l'eau s'incline en direction du bord inférieur, figure 44. I1 s'installe ainsi un écoulement d'eau dans la zone saturée induite par le gradient hydraulique (à condition de bien doser l'arrosage). fig44.eps Si les parois du bac sont transparentes et si le sable contient des grains de colorants on observe que:

• l'écoulement de l'eau affecte tout le volume du sable.
• les filets de courants sont circulaires.

On différencie dans le volume du bac de sable deux secteurs bien différents:

• secteur OA: filets de courant descendants
• secteur OB: filets de courant ascendants

Ces deux secteurs correspondent respectivement en surface, à la zone de recharge (infiltration) et à la zone de décharge (exfiltration, zone de ruissellement). Comme les filets de courant sont perpendiculaires aux lignes équipotentielles, il est possible de dessiner ces lignes. On constate alors que:

• les potentiels varient avec la profondeur
• dans la zone d'infiltration, le potentiel en profondeur est inférieur à celui de la surface
• dans la zone d'exfiltration, le potentiel en profondeur est supérieur à celui de la surface.

I1 y a lieu de se rappeler que la forme du bac, avec un rapport hauteur/longueur proche de 1, ne correspond pas à la forme d'un aquifère classique . En fait, ces observations en laboratoire correspondent parfaitement aux résultats des modèles mathématiques basés sur les équations différentielles définies ci-dessus.

Zones de recharge et zones de décharge

Considérons l'écoulement permanent dans une section en deux dimensions, en milieu isotrope et homogène, avec à la base une surface imperméable et en surface une série de collines parallèles. Si la région est humide, 1a surface piézométrique prend une forme semblable à celle de la topographie, figure 45. fig45.eps On observe que les filets de courant vont naturellement des collines en direction des vallées selon des trajectoires incurvées. Comme les trajectoires sont symétriques, il existe des verticales où il n'y a pas de composantes horizontales des écoulements : ce sont les limites d'écoulement "groundwater divides". On différencie les zones de recharge des zones de décharge en fonction de l'orientation des filets de courant (descendants ou ascendants), relativement à la surface piézométrique. On observe également que cette surface piézométrique est séparée de la surface topographique en zone de recharge alors qu'elle se confond avec elle dans les dépressions topographiques en zone de décharge. La figure 45 illustre la configuration des écoulements régionaux théoriques que l'on peut utiliser, en étant prudent, pour interpréter les observations réelles faites sur le terrain. Une des limitations à la transposition du cas théorique au cas réel réside dans le type de régime, régime permanent du modèle alors que dans 1a réalité les fluctuations des recharges induisent des fluctuations de 1a piézométrie. Toutefois ces fluctuations rapportées à l'épaisseur de la nappe peuvent être faibles et ainsi négligées. En fait il est relativement fréquent dans la réalité que le système aquifère soit en équilibre dynamique, c'est à dire que l'apport d'eau à travers la zone non-saturée corresponde juste à celui nécessaire pour maintenir en équilibre la surface libre. Ainsi le modèle correspond relativement bien à la réalité.

Effets de la topographie sur les systèmes d'écoulement

Systèmes d'écoulement

L'étude du rôle de la topographie sur l'écoulement souterrain nécessite la définition du système d'écoulement. Un système d'écoulement est l'ensemble des lignes d'écoulement fictif dans lequel 2 lignes d'écoulement voisines, en 1 point quelconque du bassin, restent voisines à travers toute la surface d'écoulement, c'est à dire entre la région alimentaire et la région d'exutoire. Si on considère une surface normale à deux lignes d'écoulement, il n'y a d'écoulement à travers cette surface que dans un sens. Ainsi chaque système possède une zone de recharge et une zone de décharge connexe et continue.

Surface libre à faible pente régulière

Dans les conditions décrites plus haut (isotrope, forme de rectangle, régime permanent) il n'y a qu'un seul système d'écoulement dans une nappe à faible pente. Si l'on fait varier l'épaisseur, on observe que dans le cas d'un aquifère de faible épaisseur, les équipotentielles sont sub-parallèles à la pente, ce qui n'est plus le cas avec une grande épaisseur, figure 46. fig46.eps

Surface libre à surface irrégulière

Si l'on compare pour une même profondeur, la distribution des écoulements de l'eau dans le cas où la surface libre est à pente régulière ou à "ondulations", on observe que dans le second cas, il se forme de nombreux systèmes d'écoulement proche de la surface alors qu'en profondeur l'écoulement est plus étendu, figure 47. fig47.eps fig48.eps fig49.eps Sur la figure 48, on différencie clairement les écoulements locaux (écoulement de la colline à la dépression voisine), des écoulements intermédiaires (séparés par des écoulements locaux), et des écoulements régionaux (qui s'écoulent d'un bout à l'autre du bassin). Figure 49. La conséquence principale de cette répartition des écoulements en système réside dans le mélange d'eau d'origine très diverse dans les zones de décharge. Selon l'importance des amplitudes, les importances relatives des systèmes d'écoulement peuvent beaucoup varier, figure 49a.

Effets de la géologie sur les systèmes d'écoulement

En attribuant à des couches géologiques des perméabilités différentes, on peut également simuler numériquement les écoulements dans des systèmes hétérogènes, figures 49b et 49c. Sur la figure 49c, on observe sur les cas a) et b), la modification de la forme des lignes d'équipotentielles due à une modification de la conductivité de la couche profonde. Le cas c) indique qu'une lentille à haute conductibilité peut même créer une zone de décharge insoupçonnable et le cas b) l'effet d'un aquitard incliné. Les figures 49b, c et d sont importantes. Elles illustrent les systèmes d'écoulement dans un environnement géologique plus complexe.

Ecoulement vers les puits artésiens juillissants

Le phénomène de l'artésianisme jaillissant peut s'expliquer, sur la base des 3 simulations numériques de deux manières bien distinctes:

• la première est classique: une formation perméable inclinée, alimentée par sa surface d'affleurement, met en charge l'eau qu'elle contient si elle est située sous une formation imperméable. Si la topographie est favorable, la charge hydraulique peut devenir supérieure à la surface du sol, figure 50a.
• la seconde est différente: dans un aquifère libre, sans faire intervenir une structure géologique, la charge hydraulique peut devenir, en profondeur, supérieure à celle de la surface du sol si l'on est dans une zone de décharge liée à une dépression topographique bien marquée, figure 50b.

fig50.eps