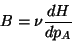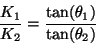


suivant: Le comportement général des
monter: Le comportement des aquifères
précédent: Types d'aquifère et drainance
Table des matières
Sous-sections
La charge hydraulique 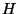 conditionne l'énergie d'un point de la nappe
d'eau. Comme l'eau se déplace du point à haute énergie vers le
point à basse énergie, il est impératif de bien connaître
conditionne l'énergie d'un point de la nappe
d'eau. Comme l'eau se déplace du point à haute énergie vers le
point à basse énergie, il est impératif de bien connaître 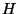 ,
si possible le champ de
,
si possible le champ de 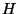 .
En laboratoire on mesure la pression généralement à l'aide de
manomètres alors que sur le terrain on utilise des tubes
piézométriques. I1 est recommandé de mettre en place en un
même endroit plusieurs piézomètres ouverts chacun à des
profondeurs différentes. On peut aussi mesurer les charges
hydrauliques correspondant à différentes profondeurs en utilisant
des packers.
fig38.eps
Sur la figure 38, on observe deux schémas de dispositif de relevé
piézométrique:
.
En laboratoire on mesure la pression généralement à l'aide de
manomètres alors que sur le terrain on utilise des tubes
piézométriques. I1 est recommandé de mettre en place en un
même endroit plusieurs piézomètres ouverts chacun à des
profondeurs différentes. On peut aussi mesurer les charges
hydrauliques correspondant à différentes profondeurs en utilisant
des packers.
fig38.eps
Sur la figure 38, on observe deux schémas de dispositif de relevé
piézométrique:
- l'un avec des piézomètres dispersés, permettant de
connaître la directionr d'écoulement et le gradient (sur ligne
de courant).
- l'autre avec des piézomètres groupés en un point afin de
connaître la composante verticale de l'écoulement.
Les cartes piézométriques donnent le champ de la charge
hydraulique H, dans une région, à un instant donné. Elles se
rapportent à un seul aquifère et on présume en représentation
2D plan que l'écoulement est horizontal.
Au point 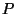 d'un liquide (figure 20), il est évident qu'une même
pression peut être obtenue avec des épaisseurs de fluides
différents selon la densité de ces derniers.
Ainsi lorsque l'on veut connaître la direction et le sens
d'écoulement de nappes captives étendues à salinité variable
ou à densité augmentant avec la profondeur, on est obligé de
prendre en compte non pas la cote de l'eau, observée dans le
piézomètre, mais
d'un liquide (figure 20), il est évident qu'une même
pression peut être obtenue avec des épaisseurs de fluides
différents selon la densité de ces derniers.
Ainsi lorsque l'on veut connaître la direction et le sens
d'écoulement de nappes captives étendues à salinité variable
ou à densité augmentant avec la profondeur, on est obligé de
prendre en compte non pas la cote de l'eau, observée dans le
piézomètre, mais 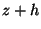 .
. 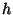 exprime la hauteur de l'eau
correspondant au niveau supérieur de la colonne d'eau douce (
exprime la hauteur de l'eau
correspondant au niveau supérieur de la colonne d'eau douce (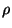 =1000
kg/m3) équilibrant la pression de référence au point
=1000
kg/m3) équilibrant la pression de référence au point 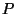 de la
nappe.
Comme
de la
nappe.
Comme
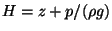 avec
avec 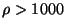 , pour une même charge,
le niveau de l'eau est plus bas lorsque l'eau est plus chargée en
sel!
Lorsque la surface libre d'une nappe est proche de la surface, on
observe des petites variations journalières du niveau statique dues
à l'intense consommation en eau des phréatophytes.
L'étude de ces variations peut être utilisée pour évaluer
l'évapotranspiration journalière, selon White (1932), figure 39.
, pour une même charge,
le niveau de l'eau est plus bas lorsque l'eau est plus chargée en
sel!
Lorsque la surface libre d'une nappe est proche de la surface, on
observe des petites variations journalières du niveau statique dues
à l'intense consommation en eau des phréatophytes.
L'étude de ces variations peut être utilisée pour évaluer
l'évapotranspiration journalière, selon White (1932), figure 39.
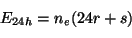 |
(4.2) |
avec
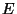 en m/jour
en m/jour
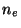 = porosité efficace en %
= porosité efficace en %
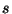 = la baisse nette du niveau statique en 24 h
= la baisse nette du niveau statique en 24 h
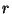 = coeff. horaire du flot ascendant (m/h)
= coeff. horaire du flot ascendant (m/h)
Durant de grands orages qui submergent d'eau de vastes étendues, on
observe souvent des remontées anormalement importantes du niveau
statique. I1 ne s'agit pas en fait d'une alimentation immédiate de
la nappe mais de la mise en charge par l'eau, qui recouvre la surface
du sol, de l'air contenu dans le sous-sol.
fig40.eps
Ainsi figure 40a, la charge dans le puits augmente après la
submersion du terrain selon les équations suivantes :
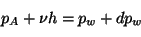 |
(4.3) |
Comme: 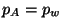 et
et 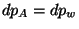 ,
on a alors:
,
on a alors: 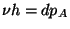 .
Si
.
Si 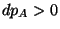 , alors
, alors 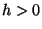 .
Les variations de la pression atmosphérique peuvent provoquer
d'importantes fluctuations de la charge hydraulique des aquifères
captifs. Selon Jacob (1940), on peut expliquer l'abaissement de la
charge hydraulique par une augmentation de la pression atmosphérique
de la manière suivante, figure 40:
Au point X :
.
Les variations de la pression atmosphérique peuvent provoquer
d'importantes fluctuations de la charge hydraulique des aquifères
captifs. Selon Jacob (1940), on peut expliquer l'abaissement de la
charge hydraulique par une augmentation de la pression atmosphérique
de la manière suivante, figure 40:
Au point X :
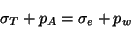 |
(4.4) |
et au point Y :
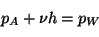 |
(4.5) |
avec
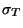 = la pression crée par le poids du terrain
= la pression crée par le poids du terrain
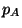 = pression atmosphérique
= pression atmosphérique
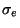 = pression sur le squelette de l'aquifère
= pression sur le squelette de l'aquifère
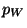 = pression de l'eau
= pression de l'eau
Si 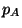 augmente, on a
augmente, on a
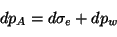 |
(4.6) |
Et 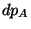 est bien sûr > à
est bien sûr > à 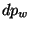 Alors
Alors
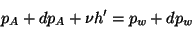 |
(4.7) |
Et
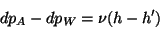 |
(4.8) |
Comme
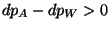 , alors
, alors 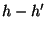 > 0 !
Dans un aquifère horizontal,
> 0 !
Dans un aquifère horizontal, 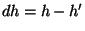 est égal à
est égal à 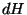 , on
qualifie alors l'influence de la pression atmosphérique par
, on
qualifie alors l'influence de la pression atmosphérique par 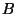 .
.
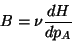 |
(4.9) |
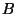 varie de 0.20 à 0.75.
Dans les aquifères libres, on observe également le même
phénomène, mais moins prononcé. On explique alors l'abaissement
de la surface libre par une augmentation de la compression de bulles
d'air prisonnières de la zone saturée.
Si le piézomètre a un diamètre relativement important, alors que
1a perméabilité du terrain est faible, le niveau dans le
piézomètre réagira avec retard à une modification rapide de la
pression (induite par exemple par un pompage ou un drainage
important).
On peut représenter l'écoulement de l'eau dans l'aquifère par
des surfaces équipotentielles et, perpendiculairement à elles, par
des lignes de courant.
En choisissant des sections parallèles aux lignes de courant, on
peut représenter en deux dimensions l'écoulement net.
On appelle ligne de courant la ligne idéale qui représente la
trajectoire théorique d'une particule d'eau en mouvement dans un
aquifère (assimilé à un niveau continu). Elle est tangente en
tous points au vecteur vitesse et en milieu isotrope, orthogonale aux
surfaces ou lignes équipotentielles.
Sur la figure 40b, la représentation classique de l'écoulement est
illustrée le long de limites classiques.
Lorsque les lignes de courant traversent des limites séparant deux
milieux à conductivité hydraulique différente, on observe une
réfraction de 1a direction d'écoulement, figure 41.
Si
varie de 0.20 à 0.75.
Dans les aquifères libres, on observe également le même
phénomène, mais moins prononcé. On explique alors l'abaissement
de la surface libre par une augmentation de la compression de bulles
d'air prisonnières de la zone saturée.
Si le piézomètre a un diamètre relativement important, alors que
1a perméabilité du terrain est faible, le niveau dans le
piézomètre réagira avec retard à une modification rapide de la
pression (induite par exemple par un pompage ou un drainage
important).
On peut représenter l'écoulement de l'eau dans l'aquifère par
des surfaces équipotentielles et, perpendiculairement à elles, par
des lignes de courant.
En choisissant des sections parallèles aux lignes de courant, on
peut représenter en deux dimensions l'écoulement net.
On appelle ligne de courant la ligne idéale qui représente la
trajectoire théorique d'une particule d'eau en mouvement dans un
aquifère (assimilé à un niveau continu). Elle est tangente en
tous points au vecteur vitesse et en milieu isotrope, orthogonale aux
surfaces ou lignes équipotentielles.
Sur la figure 40b, la représentation classique de l'écoulement est
illustrée le long de limites classiques.
Lorsque les lignes de courant traversent des limites séparant deux
milieux à conductivité hydraulique différente, on observe une
réfraction de 1a direction d'écoulement, figure 41.
Si 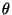 est l'angle avec la verticale, le changement de direction
s'exprime par
est l'angle avec la verticale, le changement de direction
s'exprime par
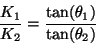 |
(4.10) |
lorsque l'eau passe du milieu de conductivité hydraulique 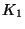 au
milieu
au
milieu 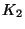 .
fig41.eps
.
fig41.eps



suivant: Le comportement général des
monter: Le comportement des aquifères
précédent: Types d'aquifère et drainance
Table des matières
2002-08-27