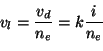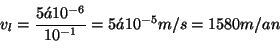


suivant: Le comportement des aquifères
monter: Le milieu souterrain et
précédent: Transmissivité et diffusivité
Table des matières
Sous-sections
D'après les unités de paramètres appliqués au mouvement de
l'eau, on peut comparer différents types de "vitesse" de l'eau.
Le rapport 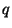 ou
ou 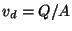 en [m/s], appelé débit spécifique
de Darcy peut être considéré comme une vitesse fictive de l'eau
à travers la section totale d'écoulement comme s'il n'y avait pas
de grains qui déforment les lignes de courant et réduisent à un
pourcentage la section d'écoulement.
I1 s'agit d'une vitesse lente. En fait dans la réalité, compte
tenu du fait que la section d'écoulement est beaucoup plus faible
que celle de l'ensemble eau-roche (elle est "encombrée" par les
grains), l'eau devra circuler beaucoup plus rapidement dans les
cheminements disponibles pour "conserver" le même débit.
Par exemple, en supposant une formation alluvionnaire, on peut
calculer vD en divisant le débit transitant par la section
d'écoulement:
en [m/s], appelé débit spécifique
de Darcy peut être considéré comme une vitesse fictive de l'eau
à travers la section totale d'écoulement comme s'il n'y avait pas
de grains qui déforment les lignes de courant et réduisent à un
pourcentage la section d'écoulement.
I1 s'agit d'une vitesse lente. En fait dans la réalité, compte
tenu du fait que la section d'écoulement est beaucoup plus faible
que celle de l'ensemble eau-roche (elle est "encombrée" par les
grains), l'eau devra circuler beaucoup plus rapidement dans les
cheminements disponibles pour "conserver" le même débit.
Par exemple, en supposant une formation alluvionnaire, on peut
calculer vD en divisant le débit transitant par la section
d'écoulement:
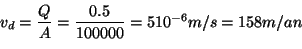 |
(3.16) |
Cette vitesse correspond à une vitesse de déplacement de l'eau
dans une direction. Cette vitesse permet par exemple de calculer le
temps de séjour de l'eau dans le sous-sol.
On calcule cette vitesse, en prenant en considération le diamètre
disponible pour l'écoulement de l'eau déduite de la porosité
efficace, figure 32 bis.
fig32b.eps
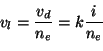 |
(3.17) |
Ainsi selon l'exemple précédent, avec une porosité de 10%, on
obtient
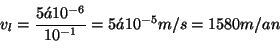 |
(3.18) |
La vitesse linéaire moyenne est donc 10 fois plus élevée.
En ajoutant à l'eau, dans un dispositif expérimental ou dans une
nappe d'eau, un traceur tel que l'uranine, on peut observer la vitesse
de déplacement de l'eau.
Même si la réception des traceurs se fait de manière dispersée
dans le temps, du fait du phénomène de la dispersion ou du rôle
des argiles absorbantes, la courbe de concentration permet de calculer
un temps de séjour et ainsi une vitesse de déplacement.
La vitesse de déplacement obtenue est comparable, en principe, à
1a vitesse linéaire moyenne.
| |
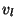 |
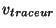 |
| sable, bassin de Paris |
3 m/an |
4m/an |
| alluvions, Rhin |
1.7 m/an |
2 m/an |
En appliquant la loi de Darcy le long d'une ligne équipotentielle,
sous forme de:
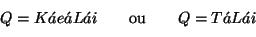 |
(3.19) |
on peut obtenir le débit de la nappe. L'évaluation des
différents paramètres par mesure sur le terrain n'est cependant
pas toujours aisée.



suivant: Le comportement des aquifères
monter: Le milieu souterrain et
précédent: Transmissivité et diffusivité
Table des matières
2002-08-27