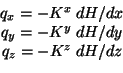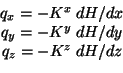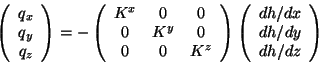


suivant: Types de milieu perméable
monter: Le milieu souterrain et
précédent: Valeurs de la conductivité
Table des matières
Sous-sections
Les valeurs de la conductivité 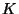 varient généralement à
l'intérieur d'une formation géologique, comme d'ailleurs selon la
direction des mesures. On appelle ceci respectivement,
l'hétérogénéité et l'anisotropie.
Si la conductivité
varient généralement à
l'intérieur d'une formation géologique, comme d'ailleurs selon la
direction des mesures. On appelle ceci respectivement,
l'hétérogénéité et l'anisotropie.
Si la conductivité 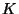 est indépendante de la position de la mesure
dans une formation géologique, on appelle cette dernière, une
formation homogène.
Si cette formation est composée de plusieurs couches de nature
différente, on aura une formation typiquement hétérogène (ex:
dépôt quaternaire classique).
On observe également souvent dans la nature un trend
d'hétérogénéité lors par exemple d'une variation latérale
de sédimentation (la perméabilité varie dans le sens de
l'écoulement).
Une formation est isotrope si la direction de mesure ne modifie pas la
conductivité mesurée. Si la conductivité
est indépendante de la position de la mesure
dans une formation géologique, on appelle cette dernière, une
formation homogène.
Si cette formation est composée de plusieurs couches de nature
différente, on aura une formation typiquement hétérogène (ex:
dépôt quaternaire classique).
On observe également souvent dans la nature un trend
d'hétérogénéité lors par exemple d'une variation latérale
de sédimentation (la perméabilité varie dans le sens de
l'écoulement).
Une formation est isotrope si la direction de mesure ne modifie pas la
conductivité mesurée. Si la conductivité 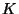 varie avec la
direction de mesure, la formation est anisotrope.
Les relations entre formations hétérogènes et anisotropes sont
illustrées par la figure 24.
fig24.eps
fig25.eps
Toutes ces définitions impliquent que l'on prenne en compte le
facteur d'échelle. Par exemple, un aquifère alluvial est
considéré comme homogène à l'échelle régionale alors qu'il
est tout à fait hétérogène à l'échelle locale et en même
temps homogène à l'échelle du V R E, (Volume Représentatif
Elémentaire), figure 25.
On distingue ainsi 3 types d'hétérogénéité:
varie avec la
direction de mesure, la formation est anisotrope.
Les relations entre formations hétérogènes et anisotropes sont
illustrées par la figure 24.
fig24.eps
fig25.eps
Toutes ces définitions impliquent que l'on prenne en compte le
facteur d'échelle. Par exemple, un aquifère alluvial est
considéré comme homogène à l'échelle régionale alors qu'il
est tout à fait hétérogène à l'échelle locale et en même
temps homogène à l'échelle du V R E, (Volume Représentatif
Elémentaire), figure 25.
On distingue ainsi 3 types d'hétérogénéité:
- 1er ordre à l'échelle du massif fissuré
- 2ème ordre à l'échelle du banc rocheux
- 3ème ordre à l'échelle de la granulométrie
La loi de Darcy 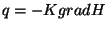 évoquée jusque là considérait
que la conductivité hydraulique ne dépendait pas de la direction
(milieu isotrope).
Dans le milieu anisotrope, on l'exprime ainsi:
évoquée jusque là considérait
que la conductivité hydraulique ne dépendait pas de la direction
(milieu isotrope).
Dans le milieu anisotrope, on l'exprime ainsi:
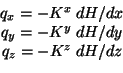 |
(3.13) |
fig26.eps
Considérant un petit cube, figure 26, on écrit la loi de Darcy,
à l'aide du tenseur des conductivités de manière suivante:
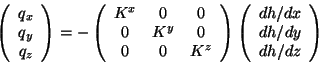 |
(3.14) |
I1 s'agit ici du cas spécial où les principales directions
d'anisotropie coincident avec les directions x, y et z (Domenico,
1990, p. 75).



suivant: Types de milieu perméable
monter: Le milieu souterrain et
précédent: Valeurs de la conductivité
Table des matières
2002-08-27